D&D battle simulator, part 2

UPDATE: I have made a website of the simulator (dnd.matteoferla.com).
SEEN ALSO: Description of battle simulator and some analysis, the GitHub code for the encounter simulator, analysis of dice equivalence

Dice equivalency

I have had several conversations about "dice equivalency" in terms of damage:
y = average value
n = number of dice
x = maximum value of dice
k = damage bonus
y = n (x+1)/2 + k
Hypothesis: all creatures with identical stats except for (n,x,k), but that do y damage have the same victory probability. The average damage is the same, the distribution of the damage is different, so under some conditions one could argue that it would differ. The simulations show there is no difference regardless of whether the fight is easy or challenging or whether there are multiple team-members.
In other words, a special weapon variant of 2d6 can be d7+d5 —assuming if you can get over the d5's ugly shape—, 2d8 –2, 3d3+1, 4d2+1 or 7, yet it will not affect the game in the very long run.

Commoner vs. giant rat

A commoner (CR0, 10 XP)  has a 7% chance of killing a giant rat CR1/8, 25 XP). The stats are:

giant_rat = Creature("Giant Rat", "evil",
                     hp=7, ac=12,
                     initiative_bonus=2,
                     attack_parameters=[['bite', 4, 2, 3]])

commoner = Creature("Commoner", "good",
                     hp=4, ac=10, 
                     attack_parameters=[['club', 2, 0, 4]])

EDIT: In my hasty typing of the stats of various monsters I mistyped the d4 of a rat bite as d3, (cf. MM p. 329), so the stats would be marginally off in favour of the peasants.
Okay, one-on-one duels are not really a thing in D&D (†), but it is a reasonable simplification as a small edge for each character becomes a large one in a party encounter. In fact, a team of four commoners has 0.5% chance against four rats, 8% against three, 52% against two and 98% against one.

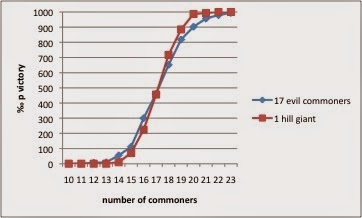
Commoners vs. hill giant

In the case of a hill giant vs. a hamlet of people, the hill giant's victory condition decreases by 22% per commoner in the linear part. It is interesting to add 17 commoners as a reference to show that the curves do differ even with an equal  midpoint.

hill_giant = Creature("Hill Giant", "evil",
                      ac=13, hp=105,
                      attack_parameters=[['club', 8, 5, 8, 8, 8], ['club', 8, 5, 8, 8, 8]])

Battle

This raises the question of what happens to the slope of x vs. y commoners. At the 4 party members each, the increase in pvictory is 31%/man in the linear portion, above a size of 4±n each this value drops only by 1%/man for each increase in team sizes. Below 4, being up or down a team members changes the odds too much, but visual inspection confirms this to be true. This means that in the x vs. y commoners scenario the steepness is the same.

This doesn't generalise to unequal numbers (4 commoners vs. 2 rats is a fair match, anything else isn't). An evil commoner with double attack or with double health will lose 60–70% of the time to two commoners (increases with hp or number), while an evil commoner with both will lose only 30% of the time.

As established, getting a character to battle against a variable amount of weenie and plotting pvictory  vs. nweenies gives a sigmoidal curve. I am not to sure about the interplay of factors and the nature of the sigmoidal curve. For now I will display the relationship between AC, HD and weapon dice as an animated gif heatmap (actually imagesc). In other words: "I have no idea, but look a pretty picture!".

†) DMing advice: never ever have a send-forth-thy-champion-to-battle-mine encounter as the tank will do his thing, while the other players build dice towers or draw new monster tokens —or worse the caster tries his hand at covert casting (a doomed mix of buff, stealth and arcana rolls required).